论文阅读：Time Series Domain Adaptation via Sparse Associative Structure Alignment

Time Series Domain Adaptation via Sparse Associative Structure Alignment（基于稀疏关联结构对齐的时间序列域自适应）

一、先验知识

Domain Adaption(域自适应)
域自适应是迁移学习中的一种代表性方法，定义是将不同领域的数据特征映射到同一个特征空间，从而利用其他领域的数据来增强目标领域的训练。

源域(source domain) 和 目标域(target domain) 共享相同的特征和类别，但是特征分布不同。源域表示与测试样本不同的领域，具有丰富的监督标注信息;目标域表示测试样本所在的领域，无标签或者只有少量标签。源域和目标域往往属于同一类任务，但是分布不同。

二、在时间序列数据集上的挑战

在解决领域自适应的问题中，目前最广泛使用的技术为提取源域和目标域的共同特征，称其为“邻域不变特征”，邻域不变特征可以让源域和目标域的分布最大限度相同，所以找到邻域不变特征，就可说明找到了源域和目标域一个共同的表示空间。

提取邻域不变特征的技术在非时间序列数据中取得了很好的性能，使用的较多的方法有RNN、LSTM等来进行特征的提取，这些方法应用在静态的、非时间序列的数据具有很好的性能，但是对于时间序列数据却难以达到很好的性能。时间滞后或偏移量的微小变化可能会导致邻域不变特征提取的困难。此外，对于多变量时间序列数据，变量并不总是等价的，现有的时间序列域自适应方法忽略了变量之间的关联结构，可能会出现过拟合的问题。

三、论文要解决的问题

1.如何摆脱时间滞后和偏移的阻碍提取稀疏关联结构?

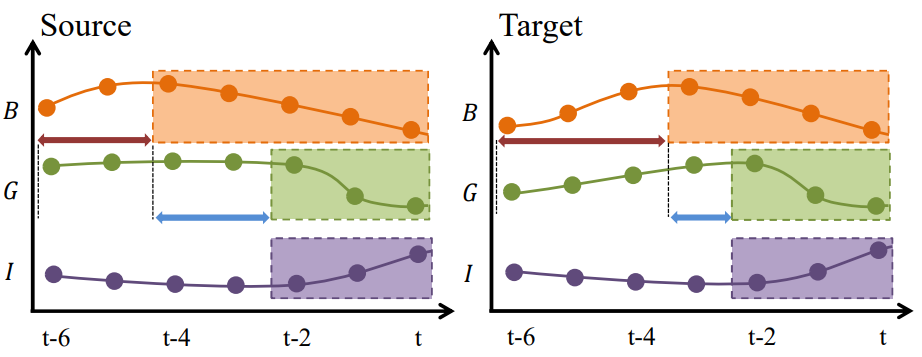
图1：“血糖(B)”、“胰高血糖素(G)”、“胰岛素(I)”三者在人体内的生理机制阐述。“血糖”的降低导致“胰高血糖素”的降低和“胰岛素”的升高。彩色块表示变量的变化段。红色双头箭头的不同长度表示不同的偏移量。蓝色双头箭头的不同长度表示“血糖”和“胰高血糖素”的不同反应时间。不同的响应时间意味着不同的时间滞后。

机体内相同的机制引起的变化却发生在不同的起始点，对于这种情况，如果仍然简单地采用神经网络作为特征提取器来提取领域不变特征，就不能排除时间滞后和偏移的负面影响，并且不能进一步提取关联结构。

所以本文需要解决的问题之一就是对于时间序列数据，面对时间滞后和时间偏移的影响，如何进行邻域不变特征的提取。

2.如何提取常见的关联结构，进一步提取邻域不变特征?

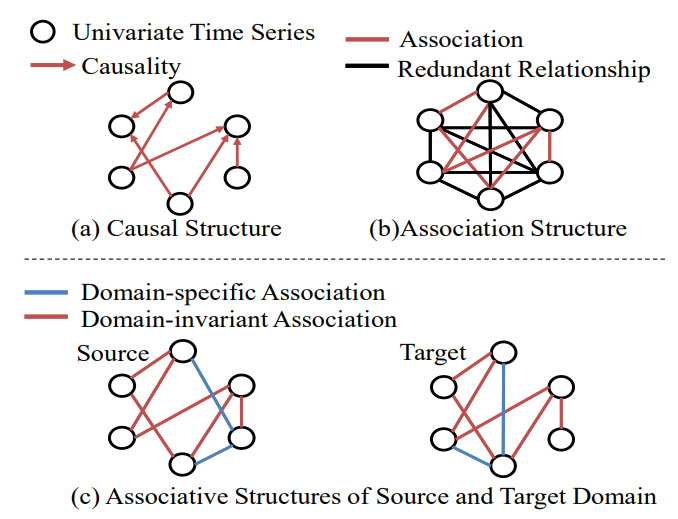
现有方法不仅考虑了ground truth关联结构，而且考虑了冗余关系，导致过拟合。由于不同域的因果结构相同，源域和目标域的时间序列数据也具有相似的关联结构。

图2© 表明考虑领域不变的关联结构并排除特定领域的关联是很重要的，并且可以使模型健壮和可推广。

然而，如何在时间序列数据中构建变量之间的关联结构是另一个挑战。现有的工作，简单地采用RNN作为特征提取器提取域不变特征，不能排除时间滞后和偏移量的负面影响，进一步无法提取关联结构。

四、模型结构

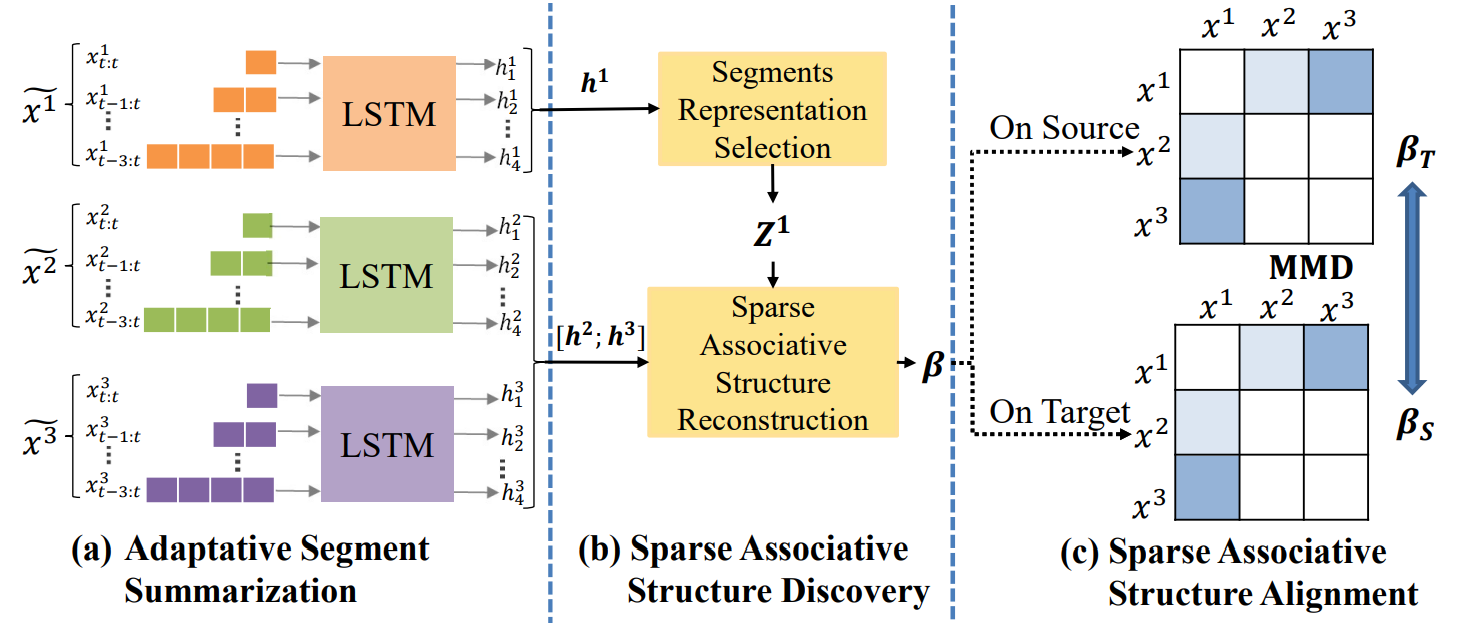
1.Adaptative Segment Summarization（自适应片段总结）

自适应分段的目的是为了消除时间滞后和偏移带来的偏差，目前现有的方法是将整个时间序列数据直接作为输入，所以说无法准确的捕捉某一段数据是从什么时候开始的，也无法准确的确定对某个因素如胰岛素造成影响的准确时间节点，所以现有的方法无法解决时间滞后和偏移的问题。

为了解决此问题，对于每个变量X都构造了多个具有不同时间长度的片段，可以从框架图种更加清晰的看出，并且为每个时间片段都分配一个独立的LSTM，即每个时间片段的数据x输入变量，输入到独立的LSTM模型中。可以得到多个参数多个时间片段的状态输出h。

2.Sparse Associative Structure Discovery（发现稀疏关联结构）

(a) 通过变量内部注意机制进行片段表征选择

进行片段表征选择首先需要使用自注意力机制，自注意力机制是注意力机制中的特殊情况，注意力机制(Attention)简单来说就是给定一个查找(query)和一个键值表(key-value pairs)，将查找映射到正确的输入的过程，由于查找、键、值和最后的结果都是向量的形式，所以输出常为加权求和的形式。论文在这一部分借助自注意力机制计算出每个参数中各个时间片段所占的权重，公式如下:

$$u^i_{\tau}=\frac{1}{N}\sum_{k=1}^{N}\frac{(h^i_{\tau}\bm{W}^{Q})(h^i_k\bm{W}^{K})^\mathsf{T}}{\sqrt{d_h}},\\ \bm{\alpha^i} = \{\alpha_1^i, \alpha_2^i,\cdots,\alpha_{\tau}^i,\cdots,\alpha_N^i\}\\=\text{sparsemax}(u^i_1,u^i_2,\cdots,u^i_{\tau},\cdots,u^i_N)$$

最终得到了参数xi的加权时间片段，除此之外，论文还考虑了某个给定的变量的时间片段持续时间随着域的改变而变化的情况，在这种情况下，为了更精确地重建关联结构，论文最小化了来自源域和目标域的a之间的最大平均差异(MMD)，以消除时间偏移带来的影响。在训练过程中，特征提取器就是要学习特征，能够使得MMD越来越小。

(b) 基于变量间注意机制进行关联结构的重构

在上一步中，通过自注意力机制提取了加权时间片段，在这一步中，论文的目标是实现变量间的稀疏关联结构的挖掘，论文采用参照注意力机制来计算两个变量之间的相关程度，需要注意的是，要考虑时间滞后的因素来计算变量相关度，公式如下:

$$\bm{e}^{ij} = \frac{Z^i \cdot Z^j}{||Z^i|| \cdot ||Z^j||}$$

$$\bm{\beta}^{i} =\{\bm{\beta}^{i1},\bm{\beta}^{i2},\cdots,\bm{\beta}^{ij},\cdots,\bm{\beta}^{iM}\}\\= \text{sparsemax}(\{\bm{e}^{i1},\bm{e}^{i2},\cdots,\bm{e}^{ij},\cdots,\bm{e}^{iM}\})(j\neq i)$$

在这里再一次使用sparsemax激活函数对参数相关度进行归一化，由此就得到了两个变量之间对时间片段的关联强度。

3. Sparse Associative Structure Alignment(稀疏关联结构对齐)

为了提取领域不变的关联结构，需要限制源域和目标域之间的结构距离，在上一步中求得的β的含义是两个参数之间的关联强度分布，所以可以将源域和目标域之间的结构距离测量转换成分布距离测量。论文中采用了领域混淆网络的思想，再次采用了MMD进行了关联结构的对比。(关联结构相邻矩阵)

五、实验结果分析

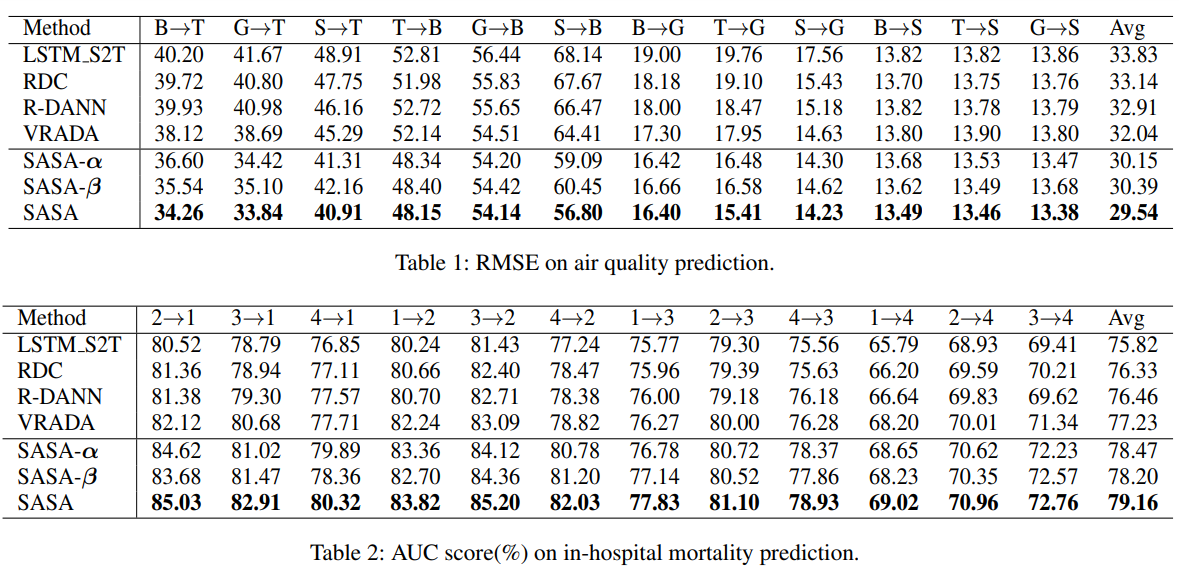
实验验证阶段，论文使用了Boiler Fault Detection Dataset、Air Quality Forecast Dataset、In-hospital Mortality Prediction Dataset三种数据集，论文将提出的方法与另外四种目前较为广泛使用的方法的实验结果进行对比。表明本论文提出的模型在所有任务上的都明显优于其他方法。

为了验证模型的每个组件的有效性，论文还进一步设计了以下模型变体。SASA-a:移除a来验证片段长度限制损失的有效性。
SASA-β:移除β来验证稀疏关联结构对齐损失的有效性。
实验结果表明，SASA-β的实验结果要比标准的SASA模型要差，论文给出的解释是因为已经提取了稀疏关联结构，而且提取的稀疏关联结构也比普通特征提取器更具健壮性和鲁棒性，但是此结构保留了特定领域的关联关系，所以才出现了变差的结果。